第1回では、ラズベリーパイを利用してのPythonの使い方、Pythonでの四則算の計算やコンピュータを利用て計算する利点などを解説しました。今回もPythonを使いながら算数や数学を学んできましょう。
人とコンピュータでの数の数え方の違い
「10」という数字は私たち人間にとって1つの区切りであり、なにかのまとまりだったり、数を数えるうえでとても重要ながいねんです。あたりまえのように0から10までを数えていますが、これはあくまで人にとって都合が良いから「10」というものを区切りにしています。10個の数字というと正確には「0,1,2,3,4,5,6,7,8,9」で10個です。
コンピュータの世界では2個の数字だけの方がとても都合がいいので、「0、1」だけを使います。なんでこのようになるのでしょうか?
今回もラズベリーパイを利用してPythonで計算をしながら理解を深めていきましょう。
人は10進法
私たち人類は10進法を使って計算します。0~9の10個の数字を使うもので、生まれたころからこの世界にいるのですべての数字がこの法則に基づいて動いている事しかしりません。「10」という数字は「9」まで数えた後に1つ位があがって、1が左について「9」が「0」に戻って「10」という事になります。
人が10進法を使うのは、元々人が数を数え始めたときに使ったのが「手」だからです。両手を使えば数を10まで数えられたから10進法が人間に都合がよかったのです。

コンピュータには2進法
ではコンピュータはなぜ「0,1」だけなのでしょうか。コンピュータは電気の世界から作られてきたものです。その根底には電磁気などがありますが、そもそもコンピュータは「スイッチ」をカチカチ切り替えて計算するところから始まっています。
人間以外に計算させる際にはシンプルに確実に状態を表現するため、スイッチが「ON」なのか「OFF」なのかで状態を表します。これは「電気が通っているか」「通っていないか」とか電気が「+」なのか「-」なのか、磁石が「N」なのか「S」なのかなどの状態に置き換えられます。
つまり、コンピュータにとって都合が良い数え方は「OFF(0)」なのか「ON(1)」なのかという2つの状態を表す「2進法」なのです。

位取り記数法(くらいどりきすうほう)
ちょっと難しそうな言葉がでてきましたが、これは簡単にいえば数の数え方とその表し方という意味です。人が使う「10進位取り記数法」とは、「0からはじまって9まで数えたら、左側に次の位(くらい)を用意して1と表して元の位を0に戻します」というふうに数を表現していきますというものです。
10進数で以下の数字を考えてみましょう。
5432 (ごせんよんひゃくさんじゅうに)
1から数をかぞえはじめて5432まで数字が積みあがっていきます。
ここで2は「一の位」といい、3はその左隣で「十の位」、4は更に左で「百の位」、5は「千の位」と左に行くほど「位(くらい)」が大きくなっていき、数も大きい状態である事がわかります。5432という数字は(ご、よん、さん、に)とただ数字がならんでいるのではなくて、数が積みあがって(ごせんよんひゃくさんじゅうに)という値をもっているものと言えます。
つまり、1000が5個、100が4個、10が3個、1が2個あるとも言い換えられます。これらを全て合わせたもの(足したもの)が5432(ごぜんよんひゃくさんじゅうに)という事になります。
Pythonで実際に計算してみましょう。
計算の順番は「( )」かっこを使って優先順位を考えて!
四則算の計算(+、-、×、÷)の計算には順番があります。かけ算やわり算というのは、先に計算すると習いました。例えば
9×2+8÷2の計算を電卓で左から順に行うと計算結果は12となりますが、通常はかけ算、わり算を優先して行います。そのためPythonで計算すると以下のようになります。
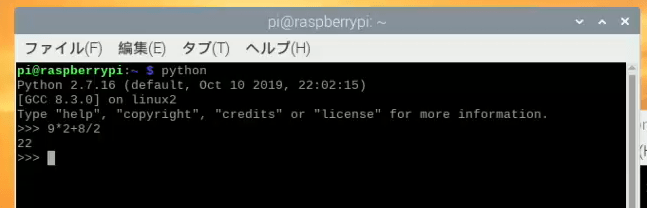
答えは22ですね。先ほど順番に計算してしまっては12が答えでした。こちらの22が正しい数字になります。
Pythonなどのプログラムを書くときには、計算過程がより分かりやすくなるように()「かっこ」を使って人が見ても分かりやすくしておいた方が良いです。
話しを元にもどして5432は1000が5個、100が4個、10が3個、1が2個ですから、計算式としては
(5×1000)+(4×100)+(3×10)+(1×2)とかっこでくくると見やすくなります。複雑な計算やプログラムを作ったときにはこのように後でどこが間違えているのかが分かりやすくしておくことが大切です。

このように、1000とか100とか10とか1はそれぞれの位の「重み」と呼んだりしています。思い出しましたか?
さて、ここで各位の数値ですが、10進数だけに10を何回掛けたかという事になります。例えば千の位であれば、10×10×10に5をかけ算しています。つまり10の3乗掛ける5という事になります。先ほどの数字を分解すると(10×10×10×5)+(10×10×4)+(10×3)+(1×2)となり、それぞれの位の重みが10の何乗かになっていることになります。
10の0乗は1
1の位だけ(1×2)と1となっているように思えますが、これは10の0乗を意味しています。かけ算ではどんな数字に0を掛けても答えは「0」になるのと一緒でどんな数字を「0乗」しても答えは「1」になります。
0乗とはゼロ回かけ算をするという意味です。10をゼロ回かけ算するというのは「10を1回もかけ算しない」という意味です。べき乗で何もしないという時は「1」にしておくことで、次のべき乗に進んだ時に計算のつじつまが合います。
例えば10の0乗が「1」なら次は10の1乗の計算を考えると、10を1回掛けるという意味になります。では「何」にかけ算をしたのかという事です。10を1回かけるのは1です。1に対して10を1回掛けたという事です。なので、10の0乗は1が基準となって1に10を0回かけ算したので、1という事になります。
プログラムで「べき乗」を表現するには
ここでは、べき乗の計算を行ってみます。先ほどの10のゼロ乗を行う場合、
>>> 10**0
とアスタリスク「*」を2回続けると計算できます。

ちなみにゼロ乗はどんな数字でも答えが「1」になるので、15のゼロ乗でも答えは「1」です。
10進数から2進数への変換
ここでは10進数を2進数に変換する方法を考えていきます。おさらいですが10進数は「0から9」までの10個の数字で数を表すため、その基数は10という事になります。2進数は「0と1」の2つの数字で表すため、基数は2となります。
10進数から2進数に変換したりすることを「基数変換」と言います。
先ほどの5432という数字は(103×5)+(102×4)+(101×3)+(100×2)=5000+400+30+2=5432となります。
これは、各桁の重みを表していて、1桁目は100、2桁目は101、となり3桁目は102、4桁目は103、という事になります。この「10」が基数となっています。
2進数を10進数に変換する方法も考え方は同じです。例えば2進数で「101」を考えてみます。2進数の基数は「2」です。なので、これを上記にならって分解していくと(22×1)+(21×0)+(20×1)となり、4+0+1=5となります。2進数の101は10進数の「5」という事になります。
では、10進数を2進数に変換する計算方法を考えます。
例えば先ほどの10進数の「5」を2進数にする場合、これは10進数の数字を2進数の基数「2」でわり算をしていきます。わり算の答え(商)をさらに2でわり算していき、割れなくなったところで答えが出ます。このわり算をする際にあまりが出たらそれがその桁の「1」になります。
5÷2=2(あまり1)です。1回目のわり算のあまりは1桁目の数字になり「1」。ここでの商は2です。続いて
2÷2=1(あまり0)です。2回目のわり算は2桁目の数字になり、ここでは「0」。商は1です。さらに
1÷2=0(あまり1)です。3回目のわり算は3桁目の数字になり、ここでは「1」。商は0で終了です。
この余りをならべると101となります。
Pythonの便利な関数
Pythonにはこれらを計算してくれる関数が用意されています。bin()関数というもので、2進法の事を「Binary (バイナリ)」と言うためbinとなっています。()の中に10進数を入れると値を返してくれます。早速 bin(5)とやってみると、

10進数の「5」は2進数では「101」でした。ここでは’0b101′ となっていますが、「0b」と先頭についているのは「バイナリーですよ」という意味になります。
まとめ
今回は四則算の順番とコンピュータの基本的な考えの元となる「2進数」を学びました。今まで私たちは10本の指を持つために10進法という概念で数を数えてきたわけですが、コンピュータはONとOFFだけを表現する2進数を使い高速に計算しています。
第3回では、この2進数と10進数の間にはいって、コンピュータの数字の数え方をより簡単に表現できる「16進数」について学び、少しプログラムも書いていきます。

